上一次和大家分享了数组公式的基础知识，今天继续分享有关数组公式的运算原理方面的内容。

【Excel基础知识】数组公式并不只属于高手（上篇）

要理解数组之间的运算原理，必须了解数组的维度和方向。

如果使用逗号分隔各个项，将创建水平数组（一行）。

如果使用分号分隔项，将创建垂直数组（一列）。

若要创建二维数组，应在每行中使用逗号分隔项，并使用分号分隔每行。

重要提示：要学明白这一课，光看不行，得动手，还得动脑。

用三个例子来说明这个问题。

示例1：

{1,2,3,4}是一个单行数组，数组中的值以逗号分隔。

选择同一行的6个单元格，输入公式={1,2,3,4}，同时按下Ctrl+Shift+Enter组合键，结果如图所示。

因为数组中只有四个数据，所以前四个单元格依次显示数组中对应的数据，后面两个单元格是错误值。

选中同一列的6个单元格，输入同样的公式，结果如图所示。

因为数组的方向与单元格的方向不一致，所以单元格中得到的都是数组中第一个数据。

示例2：

{1;2;3;4}是一个单列数组，数组中的值以分号分隔。

选择同一行的6个单元格，输入公式={1;2;3;4}，同时按下Ctrl+Shift+Enter组合键，结果如图所示。

因为数组的方向与单元格的方向不一致，所以单元格中得到的都是数组中第一个数据。

选中同一列的6个单元格，输入同样的公式，结果如图所示。

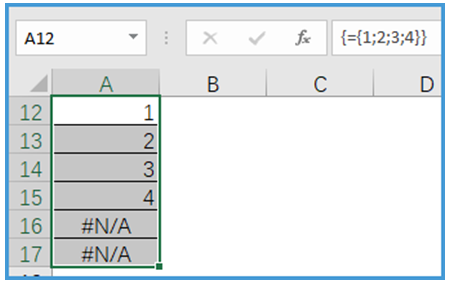
因为数组中只有四个数据，所以前四个单元格依次显示数组中对应的数据，后面两个单元格是错误值。

示例3：

{1,2,3,4;5,6,7,8}是一个两行四列的数组，逗号代表同一行，分号代表同一列。

在一个单元格区域中，同时按下Ctrl+Shift+Enter组合键输入公式={1,2,3,4;5,6,7,8}，结果如图所示。

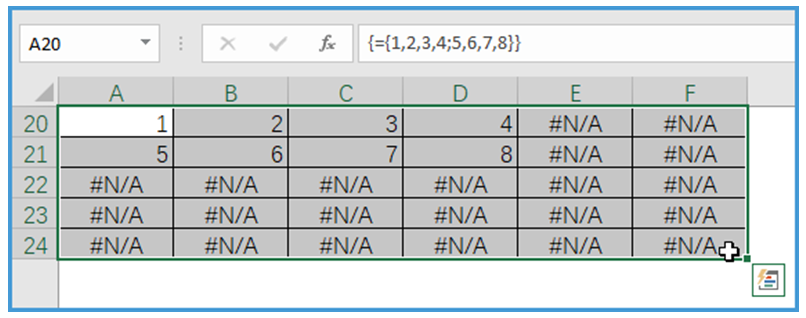
在区域左上角的两行四列单元格中，显示数组中对应的值，超过这个范围的其他单元格都是错误值。

示例1和示例2中只有一个方向（单行或单列）的数组是一维数组，示例3中同时存在两个方向的数组是二维数组。

数组的运算规则有以下5种情况。

①单值与数组的运算规则

单值与数组中的每个值进行计算，得到与数组同方向同纬度的数据。

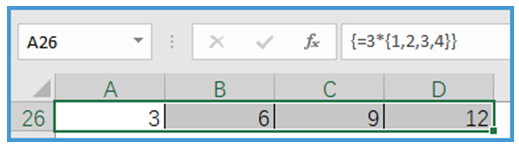
示例1：数字3与一维数组{1,2,3,4}相乘，公式为=3*{1,2,3,4}，结果如图所示。

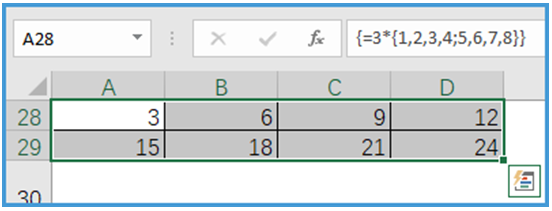
示例2：数字3与二维数组{1,2,3,4;5,6,7,8}相乘，公式为
=3*{1,2,3,4;5,6,7,8}，结果如图所示。

②同向一维数组的运算规则

两个数组中对应的数据分别计算，进行计算的两个数组中的数据个数必须相同，否则多余部分返回错误值。

示例3：数组{1;2;3}+{4;5;6}返回{5;7;9}，结果如图所示。

示例4：数组{1,2,3,4}+{4,5,6}返回{5,7,9,#N/A}，结果如图所示。

③异向一维数组的运算规则

数组1的每一个数据与数组2的每一个数据分别运算并返回结果，得到两个数组的行数*列数个元素，也就是M行数组与N列数组运算结果为M*N的矩阵数组。

示例5：数组{1;2;3}+{4,5,6,7,8}，执行1+4、1+5……1+8、2+4、2+5……3+8，结果如图所示。

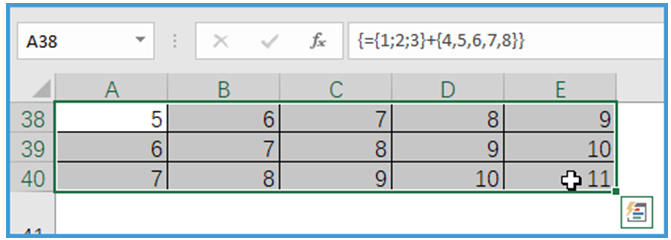
④ 一维数组与二维数组的运算规则

二维数组其中一个方向与一维数组同向同尺寸，比如M*N的二维数组与M行或者N列的数组运算，在同向的运算类似同向一维数组之间的位置对应，在异向的运算则类似单值与数组之间的一一运算。超出尺寸范围都返回错误值。

示例6：数组{1,2,3,4}+{1,2,3,4,5;6,7,8,9,10}，即四列一维数组与两行五列二维数组相加，列方向上两个数组运算按位置一一对应的，不足部分用#N/A补齐，行方向上则是一对多的运算，结果如图所示。

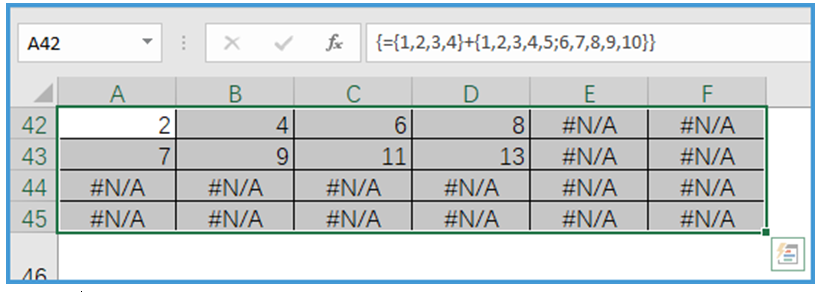
提示：结果中的2、4、6、8为第一个数组中的数据与第二个数组中的1、2、3、4相加所得；结果中的7、9、11、13为第一个数组中的数据与第二个数组中的6、7、8、9相加所得；其他位置无法对应均返回错误值。

⑤二维数组之间的运算规则

要求参加运算的二维数组具有相同的尺寸，相同位置的数据一一对应进行计算，无法对应的位置则会返回错误值。

示例7：数组{1,2;3,4}+{1,2,3,4,5;6,7,8,9,10}即两行两列的数组与两行五列二维数组相加，数组中相同位置一一对应相加，无法对应的部分用#N/A补齐，结果如图所示。

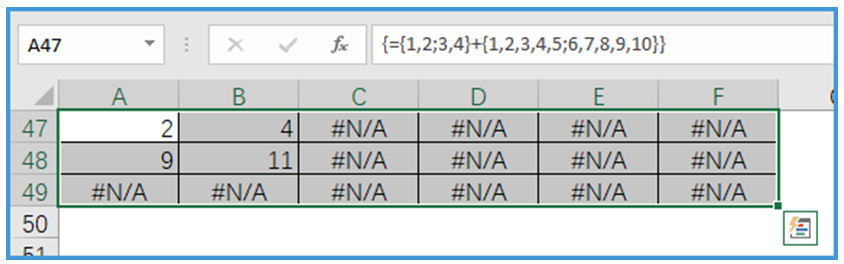
数组的维度和运算规则属于公式应用中比较有难度的部分，初学阶段只需要了解逗号和分号与数组方向之间的关系，掌握一维数组之间的计算规则即可，随着使用经验的增加，再慢慢去理解其他计算规则。